Line segment Calculator

This tool calculates and plots a line segment graph. Calculated properties include length, midpoint, slope, normal vector and perpendicular bisector. It also calculates its explicit, parametric and vector equations.

Share calculation and page on

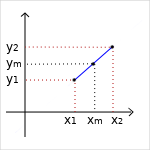
Line segment Formulas

Notations :
S : a line segment in a cartesian plane
(x₁ , y₁) : coordinates of S's starting point
(x₂ , y₂) : coordinates of S's endpoint point

Line segment length

`L = sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

Line segment slope

Segment slope is defined when `x_2 != x_1` (non vertical line segment)

`m = (y_2-y_1)/(x_2-x_1)`

Explicit Equation of line segment

We assume that `x_2 != x_1` (i.e., segment S is not vertical)

m is the slope of segment S defined above,
Let p defines as `p = y_1 - m*x_1`

Then, an explicit equation of segment S can be written as follows:

`y = mx+p , x in [x_1,x_2]`

We assume that `x_1 < x_2` otherwise, replace `[x_1,x_2]` by `[x_2,x_1]`.

Vector equation of a line segment

Segment S consists of all points M such that:
`\vec(OM) = \vecu + t \vecv \text{ } t in [0,1]` ,
`\vecu = ( x_1 , y_1 )`
`\vecv = ( x_2-x_1 , y_2-y_1 )`

Parametric equation of a line segment

This equation is derived from the vector equation (see above). A point M with coordinates (x, y) belongs to the line segment S if and only if,

`x = x_1 + t*(x_2-x_1)`
`y = y_1 + t*(y_2-y_1)`
`t in [0,1]`

Midpoint of a line segment

The coordinates of the midpoint of segment S are as follows,
`x_m = (x_1+x_2)/2`
`y_m = (y_1+y_2)/2`

Perpendicular bisector of a line segment

We assume the following:
* `y_2 != y_1` and `x_2 != x_1` (i.e. segment S is neither horizontal nor vertical)
* m : slope of segment S (defined above)
* (`x_m` , `y_m`) : coordinates of the midpoint of S (defined above).

Then, the equation of the perpendicular bisector is:

y = n.x + q

Where n and q represent the slope and y-intercept, respectively. They are defined as:
`n = -1/m`
`q = y_m - n*x_m`

Normal vector of a segment

The Normal vector `\vecn` of segment S is orthogonal to the vector that originates from the starting point and ends at the endpoint of S,

`\vecn` : (`y_1-y_2` , `x_2-x_1`)