Two circles Calculator

Two circles Calculator : points of intersection, intersection area and radical axis position.

Share calculation and page on

Two circles Formulas

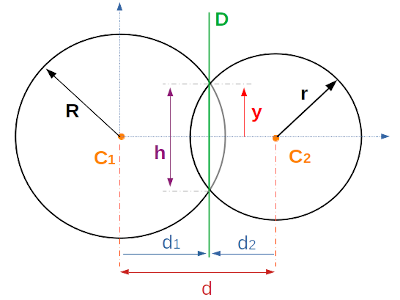
In all the following, we use the coordinates system defined by,
• the origin is C₁, the center of the circle on the left.
• x-axis is the line passing through the two centers
• y-axis is perpendicular to x-axis and passing through C₁

`d_1` is both,
• the common abcissa of the two intersection points.
• the distance between the center point C₁ and D line.

`d_1 = (R^2-r^2+ d^2)/(2*d)` `d_2 = d-d_1`

y is the ordinate of the intersection point above x-axis. So, the intersection points have the following coordinates (d₁ , y) and (d₁ , -y).
By applying pythagoras theorem, we have,

`y = sqrt(R^2 - d_1^2)` We get h, the distance between the intersection points, `h = 2*y`

Area of two circles intersection formula

This formula is deduced from Calculation formulas of a circular segment by summing areas of the two circular segments delimited by line D (radical axis).

`A = r^2arccos(d_1/r)-d_1sqrt(r^2-d_1^2)+R^2arccos(d_2/R)-d_2sqrt(R^2-d_2^2)`

Radical axis of two circles

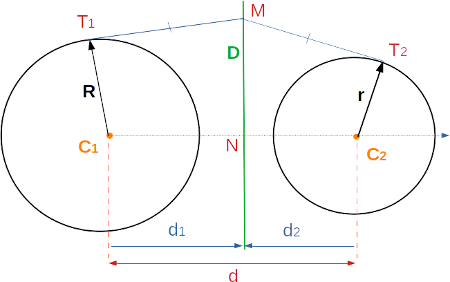
two-circles

Definition

Two circles radical axis is the line that lies between these circles and whose points have the same power with respect to the two circles. That means that tangents to the two circles, issued from each point of this line are equal.

For example, on the above diagram, D is the radical axis. (MT₁) and (MT₂) are tangent to the two circles issued from M. So, we have, MT₁=MT₂.

Calculation of the radical axis position (d₁ and d₂)

`MT_1 = MT_2` (by definition) (1)

The four following formulas are obtained by applying Pythagoras theorem to rectangle triangles MC₁T₁ , MC₂T₂ , NMC₁ and NMC₂.

`MC_1^2 = MT_1^2+R^2` (2)

`MC_2^2 = MT_2^2+r^2` (3)

`MC_1^2 = d_1^2+NM^2` (4)

`MC_2^2 = d_2^2+NM^2` (5)

We deduce from (1) , (2) and (3),

`MT_1^2 = MT_2^2 = MC_1^2-R^2 = MC_2^2-r^2` (6)

We deduce from (4) and (5),

`NM^2=MC_1^2-d_1^2=MC_2^2-d_2^2` (7)

we get from (6) and (7),

`MC_1^2-MC_2^2 = d_1^2-d_2^2= R^2-r^2` (8)

We have, `d_1+d_2 = d` (9)

By solving the two-equation system (8) and (9) with unknowns d₁ and d₂, we get,

`d_1 = (d^2+R^2-r^2)/(2d)` `d_2 = (d^2-R^2+r^2)/(2d)`

Case of two intersecting circles in two points
This is the case on the diagram at the top of the current page. Then, the radical axis is the line passing through the two intersection points.

Applications

Some applications of this calculator,
• Calculation of a crescent area
• In geometrical optics in order to calculate geometric parameters (area, height ...) of an optical lens (represented in 2D as an intersection of two circles).