Newton's thin lens equation

This calculator is the Newton's version of the thin lens equation. It computes the position of the image of an object through a thin lens with distances measured from focal points.

To calculate the image position with distances measured from the lens, use this version Gaussian thin lens equation.

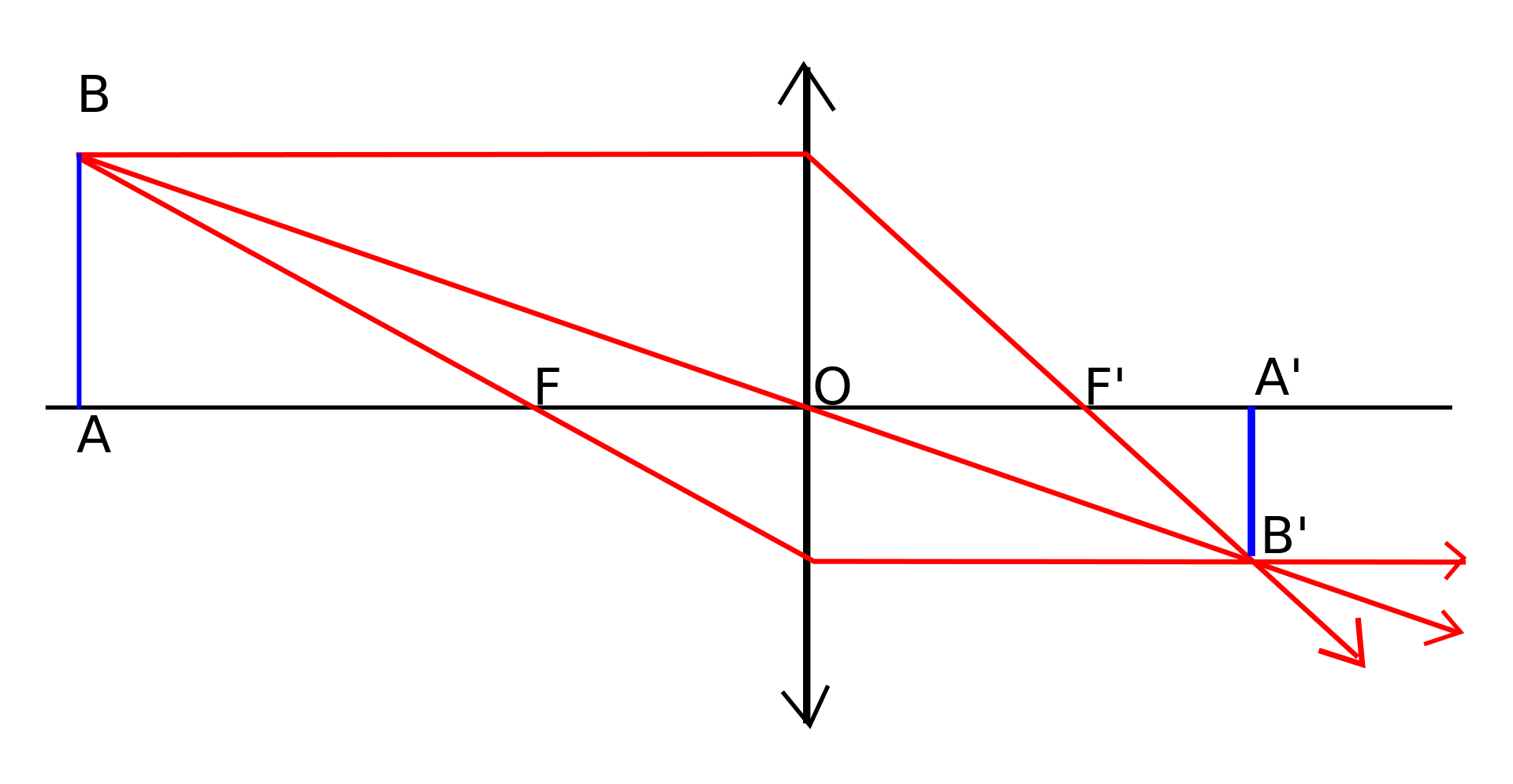
x₀ : distance from the object to the first focal point in cm (directional distance AF in the diagram)
x₁ : distance from the image to the second focal point in cm (directional distance F'A' in the diagram)
f : focal length in cm (OF' in the diagram)
All these distances obey the sign convention below.

Sign convention :
- Object and image distances are measured from the lens focal points.
- The direction of light (from object to lens) is considered as the 'positive direction' (always from left to right).

The Newton's thin lens formula is then expressed as follows,

`x_0 * x_1 = f^2`

Example : Calculate the position of the image in the case of a convergent lens

Let's calculate the position of the image of an object located 5 cm to the left of the first focal point of a converging lens. The focal length of the lens is 4 cm. So we have,
- x₀ = AF = 5 cm
- focal length: f = 4 cm
We use the calculator and get (enter "x" in the field F'A'),
x2 = 3.20 cm

The image is a real image located to the right of the second lens focal point at a distance of 3.20 cm, that is 3.20+4 = 7.20 cm to the left of the lens.

See also

Descartes conjugation relationship
Lens optical power calculator
Optics calculators