Law of Refraction
Calculator of the law of refraction also known as Snell's law.
Enter 'x' in the field to be calculated.
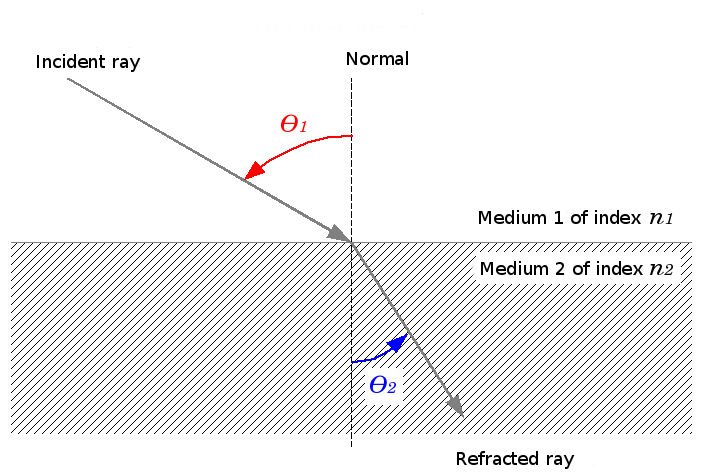
This tool is a calculator of the law of refraction (Snell's law) :
`n_2*sin(theta_2) = n_1*sin(theta_1)`
n1 : Medium 1 refractive index (incident ray)
n2 : Medium 2 refractive index (refracted ray)
`theta_1`: angle of incidence
`theta_2`: angle of refraction
This law describes the behaviour of a light ray when it changes mediums. Specifically, it calculates the angle of deviation of the light ray following a transition from a refractive medium of index n1 to another medium with refractive index n2.
Refraction ability and medium index
The refractive index of a medium is an indication of its ability to bend light. When a light ray travels from a medium into another one, the angle of refraction depends on the ratio between the two medium indices n1 and n2 because of,
`sin(theta_2) = (n_1/n_2)*sin(theta_1)`
Accordingly,
- if n2 > n1 : the light ray passes to a more refractive medium, then,
`sin(theta_2) < sin(theta_1)`
so the light ray will be closer to normal (`theta_2 < theta_1`). This is the case in the scheme above.
- if n2 < n1: the light ray passes to a less refractive medium, then,
`sin(theta_2) > sin(theta_1)`
so the light ray will move further from the normal (`theta_2 > theta_1`).Critical Angle and Refraction
`sin(theta_2) = (n_1/n_2)*sin(theta_1)`
We know that `sin(theta_2) <= 1` therefore,
`(n_1/n_2)*sin(theta_1) <= 1`
`sin(theta_1) <= n_2/n_1`
This equation is always satisfied when n2 > n1.
However, for n1 > n2, it is mathematiquelly possible to find values of `theta_1` such that this inequality is not satisfied ! if we enter these values into the calculator then, it will display NaN as value of `theta_2` (ie 'not a number').
In fact, for these values of `theta_1`, there is no refraction but a total reflection of the light ray which doesn't go into the 2d medium.
The angle `theta_1` at which this happens is called the critical angle of refractive and is calculated as follows (only when n2 < n1),
`sin(theta_1) = n_2/n_1`
`theta_1 = Arcsin(n_2/n_1)`
In summary, we've noticed that if n2 > n1 (light moving to a more refractive medium) then the ray of light will always be refracted closer to normal.
If n2 < n1 (light moving to a less refractive medium) then the light ray will be refracted away from normal provided that the angle of incidence does not exceed a limit (critical angle of refraction). Beyond this limit, the light ray will be fully reflected (middle 2 will act like a mirror).