Isosceles Triangle
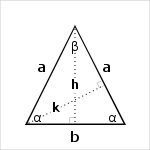
Isosceles Triangle formulas
Height from apex
In an isosceles triangle, angle bisector, median and altitude from apex to the base coincide.The common length of these lines is the height of the triangle.
Isosceles Triangle height formula is derived from Pythagorean theorem,
`h = 1/2*sqrt(4*a^2-b^2)`
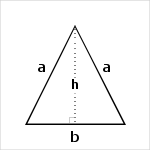
Knowing two values from a, b and h, we calculate the third one by applying these formulas,
`a = sqrt(h^2 + (b/2)^2)`
`b = 2*sqrt(a^2 - h^2)`
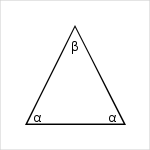
Angles
The sum of a triangle angles equals the straight angle (180 degrees or `pi` radians).So, we get,
Isosceles Triangle angles formulas :
(angles in degrees)
`2*\alpha + \beta = 180`
`\beta = 180 - 2*\alpha`
`\alpha = 90 - \beta/2`
`sin(\alpha) = cos(\beta/2) = h/a = sqrt(4*a^2-b^2)/(2*a)`
`cos(\alpha) = sin(\beta/2) = b/(2*a)`
Area
A triangle Area is equal to half of the base times height. So,
`A = 1/2*h * b`
We replace h by using the height formula (see above). We get,
`A = b/4*sqrt(4*a^2-b^2)`
Another formula to compute the area from the leg length and the apex angle is the following :
`A = 1/2 * a^2 * sin(\beta)`
`A = 1/2*h * b`
We replace h by using the height formula (see above). We get,
`A = b/4*sqrt(4*a^2-b^2)`
Another formula to compute the area from the leg length and the apex angle is the following :
`A = 1/2 * a^2 * sin(\beta)`

Perimeter
With two equal sides, the perimeter of an isosceles triangle is simply,`P = a + a + b = 2*a + b`
Périmètre d'un triangle isocèle
Le périmètre est égale à la somme des longueurs des trois côtés du triangle :`P = a + a + b = 2*a + b`
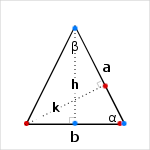
Non-principal heights (k)
These are the heights from the two ends the isosceles triangle base (length k on the diagram). We calculate alpha sine in the two triangles whose vertices are represented by blue and red points,
`sin(\alpha) = k/b = h/a`
We replace h using the formula above.
`k = b/(2a)*sqrt(4*a^2-b^2)`
`sin(\alpha) = k/b = h/a`
We replace h using the formula above.
`k = b/(2a)*sqrt(4*a^2-b^2)`
See also
Plane Geometry calculators
Geometry calculators
Mathematics calculators