Triangle isocèle
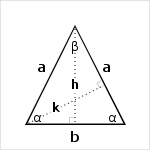
Formules de calcul dans un triangle isocèle
Hauteur issue du sommet
La hauteur issue du sommet du triangle isocèle, dite aussi hauteur principale, coincide avec :- la bissectrice issue du sommet
- la médiane issue du sommet
- la médiatrice issue du sommet
- l'axe de symétrie du triangle
La formule de calcul de la hauteur d'un triangle isocèle s'obtient à partir du théorème de Pythagore :
`h = 1/2*sqrt(4*a^2-b^2)`
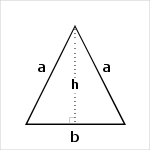
Ainsi, connaissant deux longueurs parmi a, b et h, on peut déduire la troisième :
`a = sqrt(h^2 + (b/2)^2)`
`b = 2*sqrt(a^2 - h^2)`
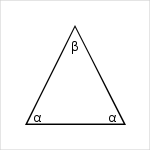
Angles
La somme des angles d'un triangle est égale à 180 degrés. On en déduit :Formules des angles dans un triangle isocèle :
(angles en degrés)
`2*\alpha + \beta = 180`
`\beta = 180 - 2*\alpha`
`\alpha = 90 - \beta/2`
`sin(\alpha) = cos(\beta/2) = h/a = sqrt(4*a^2-b^2)/(2*a)`
`cos(\alpha) = sin(\beta/2) = b/(2*a)`
Aire d'un triangle isocèle
Comme pour tout triangle, l'aire est égale au demi-produit de la base par la hauteur :
`A = 1/2*h * b`
On remplace h à l'aide de la formule ci-dessus. On obtient,
`A = b/4*sqrt(4*a^2-b^2)`
Une autre formule de calcul de l'aire à partir du côté et de l'angle au sommet est la suivante :
`A = 1/2 * a^2 * sin(\beta)`
`A = 1/2*h * b`
On remplace h à l'aide de la formule ci-dessus. On obtient,
`A = b/4*sqrt(4*a^2-b^2)`
Une autre formule de calcul de l'aire à partir du côté et de l'angle au sommet est la suivante :
`A = 1/2 * a^2 * sin(\beta)`

Périmètre d'un triangle isocèle
Le périmètre est égale à la somme des longueurs des trois côtés du triangle :`P = a + a + b = 2*a + b`
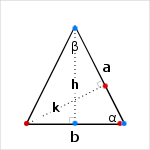
Hauteurs non principales (k)
Ce sont les hauteurs (de longueur k dans le schéma) issues des deux extrémités de la base du triangle isocèle. On les calcule à l'aide du sinus de alpha dans les deux triangles dont les sommets sont matérialisés par des points bleus et rouges,
`sin(\alpha) = k/b = h/a`
On remplace h à l'aide de la formule ci-dessus.
`k = b/(2a)*sqrt(4*a^2-b^2)`
`sin(\alpha) = k/b = h/a`
On remplace h à l'aide de la formule ci-dessus.
`k = b/(2a)*sqrt(4*a^2-b^2)`
Voir aussi
Calculateurs de Géometrie Plane
Calculateurs de Géometrie
Calculateurs mathématiques