Inverse lognormal distribution
This tool calculates the Inverse of lognormal Cumulative Distribution Function.
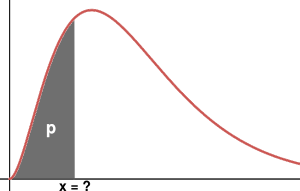
Inverse lognormal distribution formulas
X : a random variable following a lognormal distribution
`mu` : location parameter
`sigma` : scale parameter ( > 0)
The inverse of the cumulative distribution function F(x) is also called the 'quantile function', denoted Q(x). We have,
`F(x) = 1/2*(1+\text{erf}((ln(x)-mu)/(sigma*sqrt(2))))` pour `x > 0`
which inverse function is,
`Q(x) = exp(mu+sqrt(2*sigma^2)*\text{erf}^(-1)(2*x-1))`
where erf is the Error function,
`\text{erf}(x) = 2/sqrt(pi)*\int_0^x e^(-t^2)\ dt`
See also
Inverse Lognormal distribution
Lognormal distribution Chart
Statistics Calculators