Distance between a point and a line (2D and 3D)

This calculator computes the distance between a point M and a line D in a 2 or 3 dimensional space.

Share calculation and page on

How to use this calculator ?

This tool calculates the distance between a point M and a Line D.

First, choose an option in the select field,
- 2D : space of dimension 2 with coordinates axes X and Y
- 3D : space of dimension 3 with coordinates axes X Y and Z

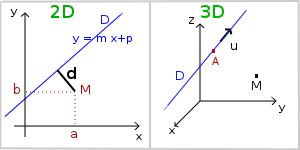
2D case :
- field 'Point M' : input the 2 coordinates of point M separated by space. For Example "4 5".
- field 'Line D' : input Line D parameters m and p, separated by space.
m is the slope and p the y-intercept.
Line D equation is y = mx+p. For example, for the line of equation y = 3x-1, input '3 space(s) -1' e.g. '3 -1'.

3D case :
- field 'Point M' : input the 3 coordinates of point M separated by space. For example "4 3 7".

In the 3D case, the line is defined by one of its points A and a parallel vector u.

- field 'Point A' : input the 3 coordinates of point A separated by space.
- field 'Vector u' : input the 3 coordinates of u, the parallel vector to line D. For Example "7 -5 1".

Distance point-line formulas

2D space :
D : a line of equation y = m x + p
M : a point of coordinates (a , b)
The distance between M and D is given by,

`d(M , D) = |b - m*a - p|/sqrt(1+m^2)`

3D space :
D is a line passing through point A and is parallel to vector u.
M is a point of 3D space.
The distance between M and D is given by,

`d(M , D) = ||vec (AM) ^^ vec u||/norm(vecu)`

`norm(vecu)` is the norm of vector u.
`||vec u ^^ vec v||` is the cross product of vectors u and v.

Distance between a point and a line (2D and 3D)

How to use this calculator ?

Distance point-line formulas

See also