Closest point on a plane

Given a plane P (Ax+By+Cz+D=0) and a point M (a b c). This tool calculates N the closest point on plane P to point M.

Share calculation and page on

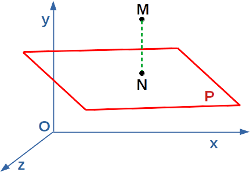
Let P be a plane of equation Ax+By+Cz+D = 0 and M a point of coordinates M (a, b, c). Let's calculate the coordinates of N, the closest point of plane P to point M.

N is the orthogonal projection of point M on plane P. We calculate the parametric equation of line (MN) by using the normal vector to plane P of coordinates (A,B,C) :

x= a +t.A
y= b +t.B
z= c +t.C

N blongs to plane P so it statisfies the équation :
A*(a+t.A) + B*(b+t.B) + C(c+t.C) + D = 0

`t = - (a.A+b.B+c.C+D)/(A^2+B^2+C^2)`

We substitue this value in the line equation to get the coordinates of N,

`x_N = a +t_N.A`
`y_N = b +t_N.B`
`z_N = c +t_N.C`

`t_N = - (a.A+b.B+c.C+D)/(A^2+B^2+C^2)`

Particular case : Closest point on the plane to origin

In this case, M and O are the same point. So, a = b = c = 0.

According to the formula above, N has the following coordinates :

`x_N = t_N.A`
`y_N = t_N.B`
`z_N = t_N.C`

`t_N = - D/(A^2+B^2+C^2)`

So, the coordinates of the closest point on the plane to origin are,

`x_N = -(D*A)/(A^2+B^2+C^2)`
`y_N = -(D*B)/(A^2+B^2+C^2)`
`z_N = -(D*C)/(A^2+B^2+C^2)`

Closest point on a plane

See also