Triangle

Triangle Calculator: you may either input side lengths and angles or vertices coordinates in 2D or 3D.

Share calculation and page on

Triangle formulas

Triangular inequality

In a triangle, the length of any side is less than the sum of lengths of the other two sides. So,

`a<= b+c`
`b<= a+c`
`c<= a+b`

Cosine law

The cosine law, also called Al-Kashi formula or generalized Pythagorean theorem, is valid for any triangle of sides a, b and c and of angles A,B and C,

`a^2 = b^2 + c^2 - 2*b*c*cos(A)`
`b^2 = a^2 + c^2 - 2*a*c*cos(B)`
`c^2 = a^2 + b^2 - 2*a*b*cos(C)`

In a right triangle with C = 90° then cos(C) = 0, we get the Pythagorean theorem,

`c^2 = a^2 + b^2`

Sine formula

We keep the same notations as above, the sine formula can be written as,

`a/sin(A) = b/sin(B) = c/sin(C)`

Triangle area

In all that follows, we denote,
a, b, c : sides lengths of the triangle
Ar : triangle area

There are several triangle area formulas. We explicit different cases.

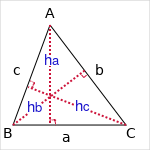
Cas 1 : we know one triangle side and the corresponding height (a and h_a or b and h_b or c and h_c).

h_a, h_b and h_c are the triangle heights issued from A, B and C.

`Ar = (a * h_a) /2 = (b * h_b) /2 = (c * h_c) /2`

Cas 2 : we know two sides lengths and their angle (for example a, b and angle C).

`Ar = 1/2*a*b*sin(C) = 1/2*b*c*sin(A) = 1/2*a*c*sin(B)`

Cas 3 : we know the sides lengths.

In this case, the triangle area can be calculated using Heron formula :

s is the triangle semi-perimeter `s = (a+b+c)/2`

`Ar = sqrt(s*(s-a)*(s-b)*(s-c))`

These are other forms of Heron formula :

`Ar = 1/4*sqrt((a+b+c)*(-a+b+c)*(a-b+c)*(a+b-c))`
`Ar = 1/4*sqrt((a^2+b^2+c^2)^2-2*(a^4+b^4+c^4))`
`Ar = 1/4*sqrt(4*a^2*b^2-(a^2+b^2-c^2)^2)`

Triangle heights

Heights `h_a` (issued from A), `h_b` (issued from B) and `h_c` (issued from C) and the triangle area are related by the following formula,

`A_r = 1/2*a*h_a = 1/2*a*h_b = 1/2*c*h_c`

Applying the Heron formula (see above), we deduce,

`h_a = 2/a * sqrt(s*(s-a)*(s-b)*(s-c))`

`h_b = 2/b * sqrt(s*(s-a)*(s-b)*(s-c))`

`h_c = 2/c * sqrt(s*(s-a)*(s-b)*(s-c))`

where s is the triangle semi-perimeter,

`s = (a+b+c)/2`

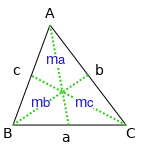
Triangle medians

Medians `m_a` (issued from A), `m_b` (issued from B) and `m_c` (issued from C) are calculated by the following formulas,

`m_a = 1/2*sqrt(2*b^2 + 2*c^2-a^2)`

`m_b = 1/2*sqrt(2*c^2 + 2*a^2-b^2)`

`m_c = 1/2*sqrt(2*a^2 + 2*b^2-c^2)`

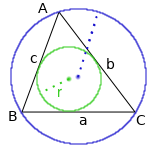
Inscribed and circumscribed circles

Triangle inscribed circle

Radius of a triangle inscribed circle (green circle of radius r) :

`r = 2*A_r/P`

`A_r` is the triangle area and P its perimeter.

By applying Heron formula (see above), we get,

Inscribed circle radius : `r = sqrt(((s-a)*(s-b)*(s-c))/s)` where s is the triangle semi-perimeter `s=1/2*(a+b+c)`

In the case of a right triangle at C, this formula is reduced to :

Radius of a right triangle inscribed circle : `r = (a+b-c)/2`

Triangle circumscribed circle

The radius of a triangle circumscribed circle (blue cercle of radius R) is calculated as,

Circumscribed circle radius : `R = a/(2*sin(A))=b/(2*sin(B))=c/(2*sin(C))`

The following formula is useful if we know the triangle three sides lengths,

Cirumscribed circle radius : `R = (a*b*c)/(4*A_r)` , `A_r` is calculated by using Heron formula (see above).

Applied to a right triangle at C, we get `R = c/2` where c is the hypothenuse length.