Right triangle

Share calculation and page on

New This calculator automatically draws the triangle to scale.

You may enter angles in different units like degree, percentage, radian and multiple of pi radian. To enter pi/6 angle, enter `\alpha` = 1/6 and choose from the units drop-down list "× pi radians".

Right triangle formulas

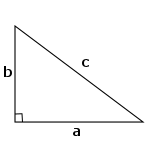
Pythagorean theorem

In a right triangle, the square of the hypotenus is equal to the sum of squares of the other two sides.

`c^2 = a^2+b^2`

The converse is also true. For a given triangle, if the square of the longest side is equal to the sum of squares of the other two sides then this triangle is right-angled.

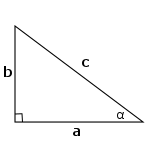
Trigonometric ratios in a right triangle

`sin(\alpha) = b / c` ; `cos(\alpha) = a / c`

`tan(\alpha) = b / a` ; `cot(\alpha) = a / b`

Less used ratios are secant (sec) and cosecant (csc).

`sec(\alpha) = c / a = 1/cos(\alpha)` ; `csc(\alpha) = c / b = 1/sin(\alpha)`

In other words,

sine = opposite side / hypotenuse
cosine = adjacent side / hypotenuse
tangent = opposite side / adjacent side
cotangent = adjacent side / opposite side

And for less used ratios,
secant = hypotenuse / adjacent side
cosecant = hypotenuse / opposite side

Complementary angles

In a right triangle, the acute angles `\alpha` and `\beta` are complementary because the sum of the three angles is 180 degrees and the third (right) angle is 90 degrees. So,

`\alpha + \beta = 90°`

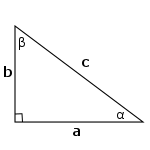
Perimeter and area

The perimeter of a triangle is simply equal to the sum of its three sides.
`P = a+b+c`

The area of the right triangle is equal to, `A = (a*b)/2`

Height Calculation

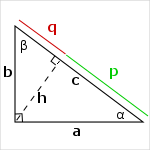
Calculating the height h from the perpendicular sides a and b

`h = (a*b)/c = (a*b)/sqrt(a^2+b^2)`

This formula is based on the similarity of the triangles (h, q, b) and (a, b, c). Therefore,

`h/b=a/c`

Right triangle altitude theorem

h : altitude (or height) on the hypotenuse
p : projection of leg a on the hypotenuse
q : projection of leg b on the hypotenuse

The square of the altitude on the hypotenuse is equal to the geometric mean of the projections of the legs (non-hypotenuse sides) on the hypotenuse.

`h^2 = p*q`

Indeed, the triangles formed by the sides (h, q, b) and (p, h, a) are similar (since they have three equal angles), therefore,

`h/q=p/h`

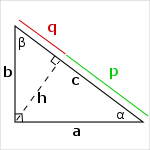
Leg geometric mean Theorem or Leg rule

The length of a leg of a right triangle is the geometric mean of the lengths of the hypotenuse and the projection of that leg on the hypotenuse.

`a^2 = p*c <=> a = sqrt(p*c)`
`b^2 = q*c <=> b = sqrt(q*c)`