Mass moment of inertia of a rectangular plate

Calculates the mass moment of inertia of a rectangular plate.
`I_z = 1/12*m*(h^2+w^2)` (about the perpendicular central axis)
`I_x=I_y = 1/24*m*(h^2+w^2)` (about a symmetry axis in the plate plane)
`I_e= 1/12*m*(4*h^2+w^2)` (about axis at the end of the plate
Enter 'x' in the field to be calculated.

Rotation axis

Moment of inertia (I)

Mass (m)

Height(h)

Width (w)

Result format

Share calculation and page on

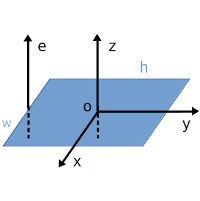
Here are the formulas to calculate the mass moment of inertia of a thin rectangular plate about different axis.

Case of a rotation about the perpendicular central axis at center of the plate (z-axis on above diagram),
`I_z = 1/12*m * (h^2+w^2)`

Case of a rotation about on of the two symmetry axis on the plate plan (x-axis and y-axis on above diagram),
`I_x = 1/24*m * (h^2+w^2)`

Case of rotation about axis at end of the plate (Me on above diagram). This axis passes through the midpoint of the width line segment (of length w) and is perpendicular to the plate plane.
`I_e = 1/12*m * (4*h^2+w^2)`

m : mass of the plate in kilogram (kg)
h : its height in meter (m)
w : its width in meter (m)

Mass moment of inertia of a rectangular plate

See also