Inverse Beta distribution
This tool calculates the Inverse of Beta Cumulative Distribution Function. One of its uses is to calculate percentiles of a Beta distribution.
Inverse Beta Distribution formulas
Notations
X : a random variable following a beta distribution
`alpha` : shape parameter (> 0)
`beta` : second shape parameter (> 0)
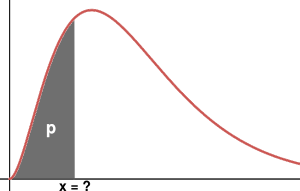
The inverse of the cumulative distribution function F(x) is also called the 'quantile function', denoted Q(x). We have,
`F(x) = (Gamma(alpha+beta))/(Gamma(alpha)*Gamma(beta))*\int_-oo^xt^(alpha-1)(1-t)^(beta-1)\ dt`
`Q(x) = F^(-1)(x)`
For a probability p, quantile function Q gives a q value that verifies,
`q = Q(p) = F^(-1)(p)`
By definition of F, we have,
`P(X < q) = p`
`P(X < q)` is the pobability that X is less than q.
See also
Gamma distribution Probabilities
Gamma distribution Chart
Statistics Calculators